มาถึงตอนที่สี่ของซีรียส์เรียนคณิตศาสตร์กับนายติวฟรีในบทเรียนภาคตัดกรวย ของ คณิตศาสตร์ ม.4 มาถึงตอนที่ตอนนี้เป็นเรื่องของสมการวงรี (Ellipse) กันแล้วนะครับ สมการวงรีเป็นเรื่องที่อาจจะเข้าใจยากในตอนแรกแต่ถ้ารู้เรื่องแล้วถือ ว่าเรียนสนุกครับ ลองมาเรียนกันนะ

วงรีคือเส้นโค้งรูปไข่ที่เหมือนการดึงวงกลมให้ยืดออกตามเส้นผ่านศูนย์กลางเส้นใดเส้นหนึ่ง
นิยามสมการวงรี
วงรี (Ellipse) คือเซตของจุดทั้งหมดในระนาบซึ่งผลบวกของระยะทางจากจุดใดๆจุดหนึ่งในเซตไปยังจุดคงที่ 2 จุดมีค่าคงตัว
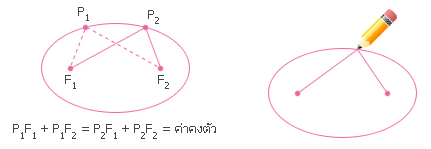
จากบทนิยามนี้ มีวิธีง่ายๆ ในการวาดรูปวงรี (ดูรูปที่ 2) วางกระดาษบนกระดานวาดรูปปักหมุด 2 ตัวที่จุดต่างกัน ใช้เป็นโฟกัสของวงรี ตัดเชือกเส้นหนึ่งยาวกว่าระยะทางระหว่างหมุดทั้งสอง ผูกปลายเชือกแต่ละข้างกับหมุด โดยใช้ดินสอรั้งเชื่อให้ตึงตลอดเวลา ขณะที่ค่อยๆ เคลื่อนดินสอรอบโฟกัส รอยดินสอที่เกิดขึ้นจะเป็นรูปวงรีเพราะผลบวกของระยะทางจากจุดปลายดินสอถึงโฟกัสทั้งสองเท่ากับความยาวของเชือกที่มีความยาวคงตัวเสมอ
ถ้าเชือกยาวกว่าระยะห่างระหว่างโฟกัสเพียงเล็กน้อย วงรีที่วาดได้จะมีรูปร่างเรียวยาว ดังเช่นในรูปที่ 3ก แต่ถ้าโฟกัสอยู่ใกล้กันเมื่อเปรียบเทียบกับความยาวของเชือก (เชือกยาวกว่าระยะห่างระหว่างโฟกัสมาก) วงรีที่วาดได้จะเกือบกลม ดังเช่นในรูปทางขวา ยิ่งถ้าจุดโฟกัสใกล้กันเท่าไหร่ ก็จะยิ่งกลมขึ้นๆ

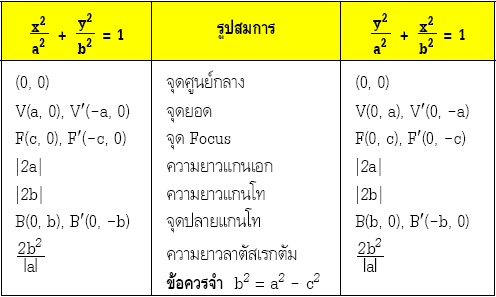
ส่วนประกอบของวงรี
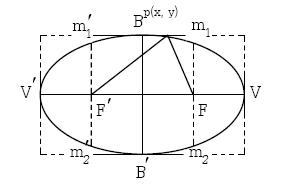 F, F’ เป็นจุดคงที่ เรียกว่าจุดโฟกัส (Focus)
F, F’ เป็นจุดคงที่ เรียกว่าจุดโฟกัส (Focus)
V, V’ เป็นเส้นตรงที่ผ่านจุดโฟกัส และมีจุดปลายทั้งสองเป็นจุดยอด เรียกว่า แกนนอก
B, B’ เป็นเส้นตรงที่ผ่านจุดศูนย์กลางและตั้งฉากกับแกนเอก โดยมีจุดปลายทั้งสองอยู่บนวงรี เรียกว่า แกนโท
m1m2, m1‘m2‘ เป็นเส้นตรงที่ผ่านจุดโฟกัส และตั้งฉากกันแกนของรูป เรียกว่าเส้นลาตัสเรกตัม
วงรีที่มีจุดศูนย์กลางอยู่ที่จุด (0,0)
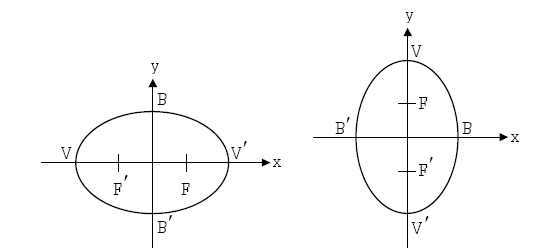
วงรีที่มีจุดศูนย์กลางอยู่ที่จุดกำเนิดและแกนเอกอยู่บนพิกัด

สรุปสมการวงรี
ตัวอย่างโจทย์สมการวงรี
EX1: วงรีรูปหนึ่งมีสมการเป็น ![]() = 1
= 1
จงหาโฟกัส จุดยอด ความยาวของแกนเอกและแกนโท และเขียนวงรี
วิธีทำ จากสมการ ![]() = 1 เมื่อเทียบกับรูปแบบมาตรฐาน
= 1 เมื่อเทียบกับรูปแบบมาตรฐาน ![]() = 1
= 1
จะได้ว่า a2 = 16, b2 = 4 นั่นคือ a = 4, b = 2
เนื่องจากพจน์ a2 เป็นตัวส่วนของพจน์ x2
แกนเอกจึงอยู่บนแกน X ถ้าให้จุด (-c, 0) และ (c, 0) เมื่อ c > 0 เป็นโฟกัส
จะได้ว่า c2 = a2 – b2 = 16 – 4 = 12 นั่นคือ c =![]()
ดังนั้น สรุปได้ว่า
โฟกัสของวงรี คือ (-![]() , 0) และ (
, 0) และ (![]() , 0)
, 0)
จุดยอด คือ (-4, 0) และ (4, 0)
แกนเอกมีความยาว 8 หน่วย
แกนโทมีความยาว 4 หน่วย
กราฟวงรีแสดงได้ดังรูปนี้
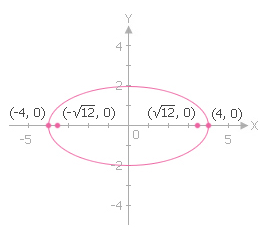
#Answer
ตัวอย่างที่ 2 วงรีรูปหนึ่งมีจุดยอดอยู่ที่ (-4, 0), (4, 0) และโฟกัสอยู่ที่ (-3, 0), (3, 0) จงหาสมการและเขียนวงรี
วิธีทำ จากสิ่งที่กำหนดให้จะได้ว่า แกนเอกของวงรีอยู่บนแกน X และเมื่อเทียบกับ
รูปแบบมาตรฐานของสมการวงรี ![]() = 1 จะได้ว่า a = 4, c = 3
= 1 จะได้ว่า a = 4, c = 3
จาก c2 = a2 – b2 จะได้ 32 = 42 – b2
b2 = 42 – 32 = 16 – 9 = 7
ดังนั้น สมการของวงรี คือ
![]() = 1
= 1
กราฟเป็นวงรีแสดงในรูปนี้
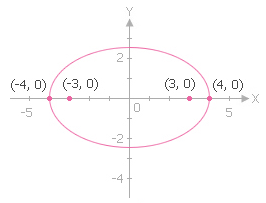
#Answer
EX3: จงหาโฟกัสและเขียนวงรีที่มีสมการเป็น 25×2 + 9y2 = 225
วิธีทำ จากสมการวงรีที่กำหนดให้ เขียนในรูปแบบมาตรฐานได้ดังนี้ ![]() = 1
= 1
จากรูปแบบมาตรฐาน จะได้ว่าแกนเอกของวงรีอยู่บนแกน Y
และ a2 = 25, b2 = 9
นั่นคือ c2 = a2 – b2 = 25 – 9 = 16
ดังนั้น c = 4 และโฟกัสของวงรี คือ (0, -4) และ (0, 4)
กราฟของวงรีแสดงในรูปนี้
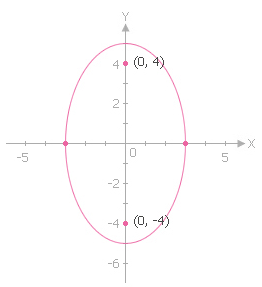
จะเห็นได้ว่า ถ้า 2a มากกว่า 2c เพียงเล็กน้อย วงรีมีรูปร่างเรียวยาว (วงรีมีความรีมาก) แต่ถ้า 2a มากกว่า 2c วงรีมีรูปร่างเกือบจะกลม (วงรีมีความรีน้อย) โดยทั่วไป จะใช้อัตราส่วนของ c ต่อ a วัดความรีของวงรี อัตราส่วนนี้เรียกว่า ความเยื้องศูนย์กลาง
ความเยื้องศูนย์กลางของวงรีมีค่าระหว่าง 0 และ 1 นั่นคือ 0 < e < 1 ถ้า e มีค่าใกล้ 1 หรือ c มีค่าเกือบจะเท่ากับ a แล้ววงรีมีความรีมาก (มีรูปร่างเรียวยาว) แต่ถ้า e มีค่าใกล้ 0 แล้ววงรีมีความรีน้อย (รูปร่างเกือบจะกลม) รูปที่ 10 แสดงวงรีที่มีความเยื้องศูนย์กลางต่างๆ กัน
ข้ามไปยังเนื้อหา:
สำหรับ คนที่สนใจอยากเรียนคณิตศาสตร์เรื่องภาคตัดกรวย และบทอื่นๆ แต่ไม่อยากอ่านเอง อยากดูในรูปแบบคลิปวีดีโอมากกว่า พี่มีของดีมาแนะนำครับ คลิปวีดีโอสอนเรื่องความน่าจะเป็นครบทุกหัวข้อ และบทเรียนอื่นๆในระดับชั้นมัธยมอีกครบถ้วน สอนอย่างละเอียดตั้งแต่เริ่มต้น พร้อมด้วยโจทย์เรื่องภาคตัดกรวยเรียงจากง่ายไปยาก ลองอ่านข้อความด้านล่างนี้ดูนะครับ
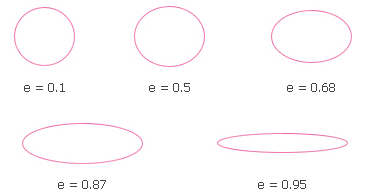


![รวมข้อสอบ O-NET ม.6 พร้อมเฉลย [Download] - Tewfree](https://www.tewfree.com/wp-content/uploads/2020/01/download-ข้อสอบ-o-net-400x209.jpg)









จัดรูปสมการวงรีแบบนี้ ทำยังไงคะ
1. 1/2 (X^2) + 1/8 (y^2) = 1/4
2. y^2 = 1-(X^2)
3. 20(X^2) + 4(y^2) = 5
โจทย์นะคะ
1. จุด P เป็นจุดใดๆบนวงรี ผลบวกของระยะทางจากจุด P ไปยังจุด (-4,0) กับจุด (4,0) เท่ากับ 12 หน่วย
2.P เป็นจุดใดๆบนวงรี ผลบวก ของระยะทางจากจุด P ไปยังจุด (-4,2) กับ (-4,8) เท่ากับ 10 หน่วย
ช่วยหน่อยค่าาาา งงมาๆกเลยย พลีสสส ฮือๆๆๆ
หนูไม่เข้าใจ
ข้อที่ 1 ทำไมจุดโฟกัสถึงติดรูด 12 ละคะ
a^2 = 16
b^2 = 4
จาก c^2 = a^2-b^ = 16-4
นั่นคือ c^2 = √12 (ติดรูทเพราะไม่ตัวตัวไหนกำลังสองแล้วได้12)
#แก้ไข
c^2 = 12
c = √12
ถามหน่อยค่ะ
y กำลัง 2=8x
ทำไงคะ